Nombres relatifs 4ème
Les nombres relatifs 4ème sont des nombres qui possèdent un signe positif (+) ou un signe négatif (–). Ils permettent de représenter des situations de la vie courante comme :
les températures (–5 °C, +10 °C),
les altitudes (–100 m, +250 m),
les comptes bancaires (–50 €, +200 €).
Ils élargissent l’ensemble des nombres et offrent un moyen simple de modéliser des phénomènes qui se situent au-dessus ou en dessous d’un point de référence.
1. Addition et soustraction de nombres relatifs
Cours
Somme de deux nombres relatifs
Propriété : Pour effectuer la somme de deux nombres relatifs de même signe:
- on garde le signe commun aux deux nombres
- on additionne les distances à zéro des deux nombres
Illustration :
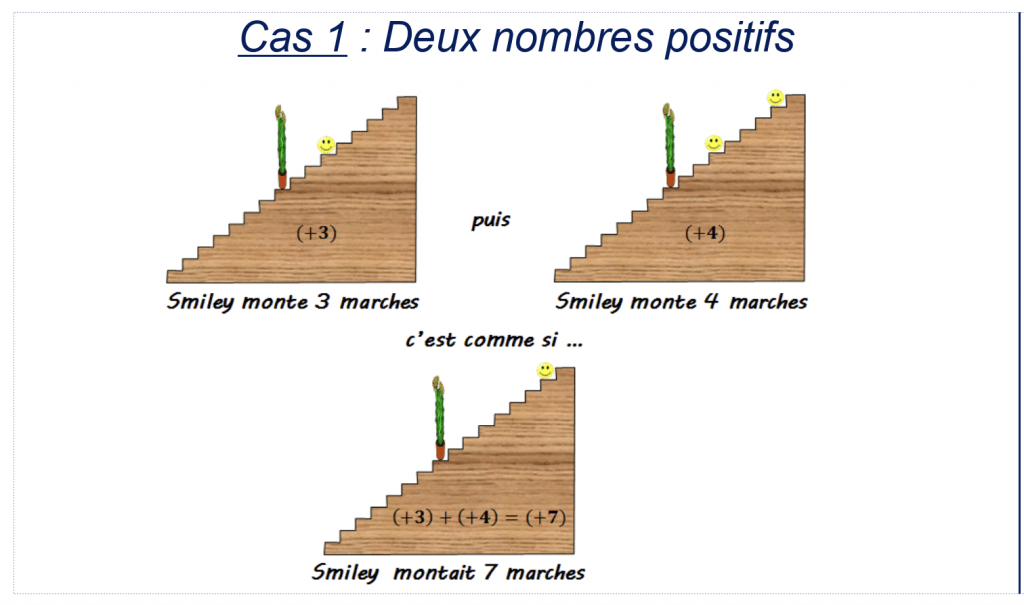
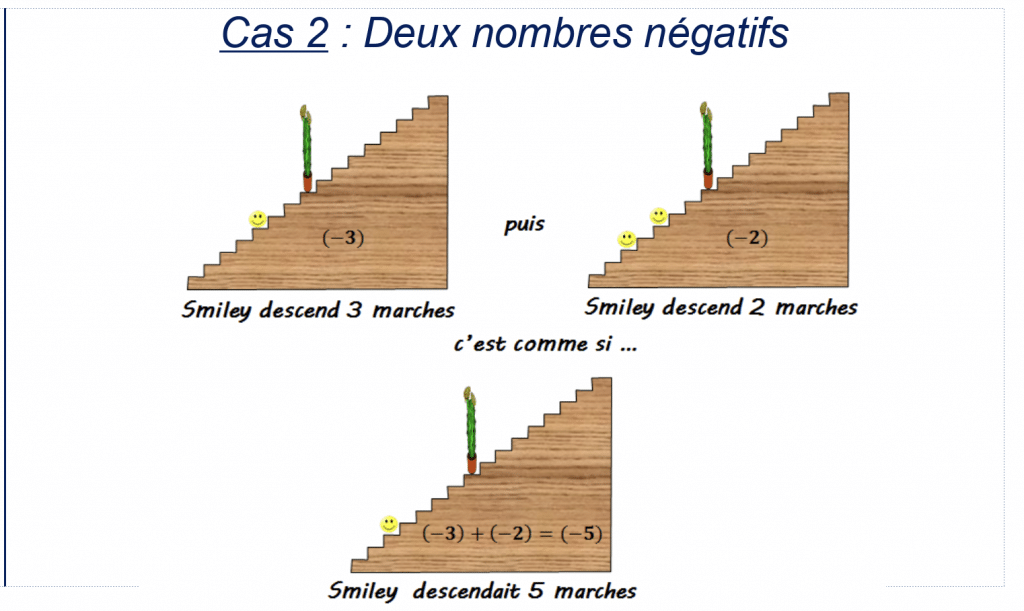
Exemple : Calculer.
A = (-6)+(-10) = -16
B = (+2)+(+4) = +6
Propriété : Pour effectuer la somme de deux nombres relatifs de signes contraires:
- on garde le signe du nombre qui a la plus grande distance à zéro
- on soustrait les distances à zéro des deux nombres
Illustration:
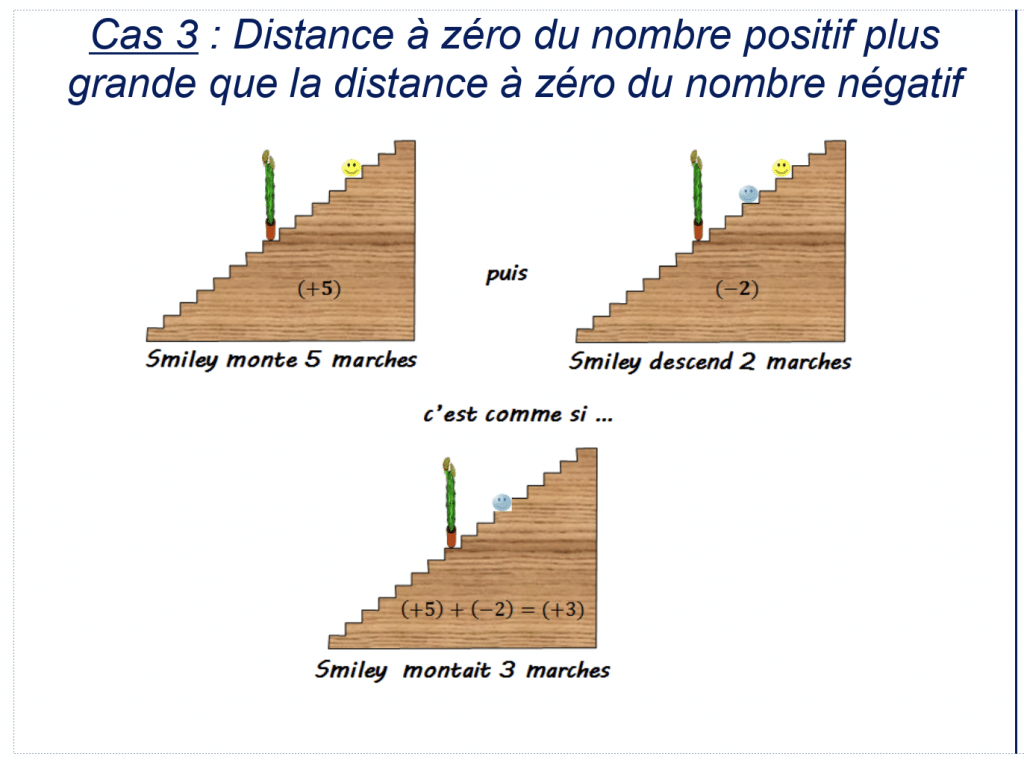
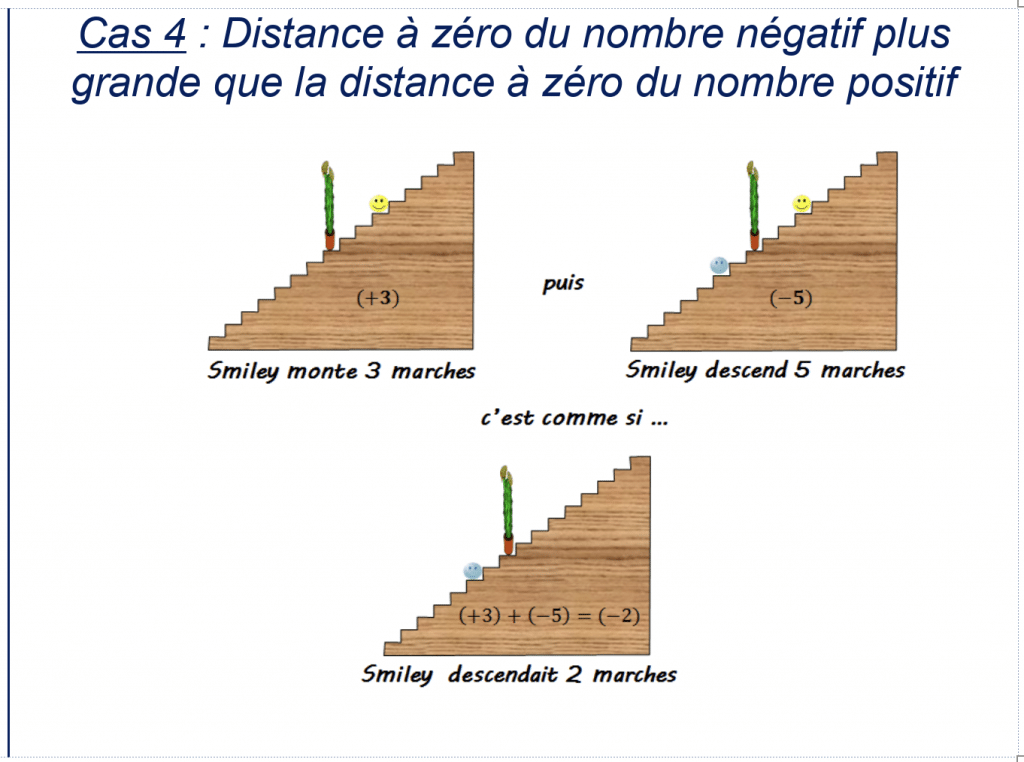
Exemple : Calculer.
C = (+4)+(-7) = -3
D = (-3)+(+10) = 7
Différence de deux nombres relatifs
Propriété : Soustraire un nombre relatif revient à ajouter son opposé.
Exemple :
E = (-2) – (+4) = (-2) + (-4) = -6
F = (+6) – (-5) = (+6) + (+5) = 11
Exercices d'application
Nombres relatifs – Additions et soustractions de deux nombres relatifs.pdf
Correction des exercices d’application :
Cours
Somme algébrique
Méthode: On peut calculer une somme algébrique en effectuant les calculs de gauche à droite. Cependant, afin de gagner du temps, il sera plus judicieux de regrouper les nombres positifs ensembles et les nombres négatifs ensembles afin de calculer plus rapidement.
Exemple: Calculer l’expression suivante.
A = (-13) – (-9) + (-7) – (+4) + (+11)
A = (-13) + (+9) + (-7) + (-4) + (+11)
A = (+20) + (-24)
A = – 4
Remarque: Quand dans une suite d’additions, il apparaît deux nombres opposés on peut les supprimer car leur somme est égale à zéro.
Écriture simplifiée d'une somme
Simplifier l’écriture d’une somme de nombres relatifs, c’est supprimer :
- Les parenthèses autour des nombres relatifs
- Les signes d’addition entre les parenthèses
- Le signe « + » devant le premier terme s’il est positif
Exemple : Calculer les expressions suivantes en repassant par une écriture non simplifiée.
B = -2 – 5 signifie B = (-2) + (-5) = -7
C = -4 + 6 signifie C = (-4) + (+6) = 2
D = 8 + 3 signifie D = (+8) + (+3) = 11
E = 5 – 9 signifie E = (+5) + (-9) = -4
Exercices d'application
Nombres relatifs – Somme algébrique.pdf
Correction des exercices d’application :
2. Produit de nombres relatifs
Cours
Produit de deux nombres relatifs
Propriété : Pour effectuer le produit de deux nombres relatifs:
- on détermine le signe du produit :
- si les deux nombres sont de même signe , le produit est positif.
- si les deux nombres sont de signe contraire, le produit est négatif.
- on multiplie leurs distances à zéro.
La méthode pour déterminer le signe d’un produit de deux nombres relatifs est appelée règle des signes.
Exemple : Calculer.
F = – 2 x 11 = – 22
G = 9 x (-8) = – 72
H = – 5 x (-7) = 35
Remarques :
- Si on multiplie un nombre par -1 , on obtient son opposé.
- Si l’un des facteurs d’un produit vaut 0, alors le produit vaut 0.
Produit de plusieurs nombres relatifs
Propriété : Dans un produit de plusieurs facteurs,
- si le nombre de facteurs négatifs est pair , alors ce produit est un nombre positif.
- si le nombre de facteurs négatifs est impair, alors ce produit est négatif.
Exemple: Calculer les expressions suivantes.
I = -2 x 3 x (-5) = 30 ; Le résultat est positif car il y a 2 facteurs négatifs dans cette expression. 2 étant un nombre pair.
J = -1 x 2 x (-3) x 4 x (-5) = – 120 ; Le résultat est négatif car il y a 3 facteurs négatifs dans cette expression. 3 étant un nombre impair.
Exercices d'application
Nombres relatifs – Produit de nombres relatifs.pdf
Correction des exercices d’application :
3. Quotient de nombres relatifs
Cours
Propriété : Pour effectuer le quotient de deux nombres relatifs (le diviseur étant différent de 0),
- on détermine le signe du quotient en appliquant la règle des signes de la multiplication
- on divise leurs distances à zéro.
Remarque : Il est possible que le quotient des distances à zéro n’admette pas d’écriture décimale car la division ne s’arrête pas. On peut cependant donner une valeur approchée de ce quotient.
Exercices d'application
Nombres relatifs – Quotient de nombres relatifs.pdf
Correction des exercices d’application :
Pour plus de vidéos, découvrir la chaine Youtube FormaMaths.
Les nombres relatifs 4ème permettent de représenter et de calculer avec des valeurs positives et négatives. En maîtrisant leurs règles d’addition, de soustraction, de multiplication et de division, tu pourras résoudre des situations concrètes et progresser en mathématiques.
Prochaines Étapes
La pratique régulière est essentielle pour se familiariser avec les nombres relatifs. Pour exceller :
Révisez attentivement les exercices corrigés pour vous familiariser.
Poursuivez votre progression en explorant les autres chapitres de 4ème.
N’hésitez pas à utiliser les ressources complémentaires sur la chaîne Youtube FormaMaths pour des explications visuelles ou bien prendre des cours particuliers. Vous pouvez essayer des maintenant gratuitement et sans condition nos cours particuliers.
