Notion de fonction 3ème
Les fonctions sont un concept fondamental des mathématiques. Elles permettent de décrire une relation entre deux grandeurs, c’est-à-dire comment une valeur dépend d’une autre.
Par exemple, si on double un nombre, la fonction qui associe chaque nombre à son double permet de modéliser cette relation.
Dans ce chapitre, nous allons apprendre à :
- Savoir ce qu’est une fonction
- Trouver l’image et l’antécédent d’un nombre par le calcul, par lecture d’un tableau de valeur et par lecture graphique.
1. Notion de fonction
Cours
Définition : Une fonction est un procédé qui, a un nombre, associe un seul autre nombre.

Notation : On considère une fonction . Si on appelle « x » la variable, le nombre qui lui est associé se note f(x) et se lit « f de x ».

On note aussi f: x –> f(x); ce qui se lit « la fonction f, qui à x, associe f(x)».
Exemple : Soit la fonction f définie par l’égalité : f(x) = 7x – 5
Ce que l’on note aussi f: x –> 7x – 5
Remarque : « x » est un nombre. « f » désigne une fonction ; « f » n’est pas un nombre !
2. Image et Antécédent
Cours
Définition : On considère une fonction .
Le nombre de départ « x » est appelé antécédent.
Le nombre d’arrivée « f(x) » est appelé l’image de « x ».
Exemple : Soit la fonction f définie par l’égalité : f(x) = 7x – 5
- Quelle est l’image de 3 par la fonction f ?
Pour calculer l’image d’un nombre, il suffit de remplacer la lettre « x » par le nombre dont on veut trouver son image.
Dans notre cas, il suffit de remplacer dans la fonction la lettre « x » par « 3 ».
f(3) = 7 x 3 – 5 = 21 – 5 = 17.
L’image de 3 par la fonction f est 17.
- Quelle est l’antécédent de 9 par la fonction f ?
Pour déterminer l’antécédent d’un nombre, il suffit de résoudre une équation.
Dans notre cas, l’équation à résoudre est la suivante : f(x) = 9.
f(x) = 9 ;
7x – 5 = 9
7x – 5 + 5 = 9 + 5
7x = 14
7x/7 = 14/7
x = 2
L’antécédent de 9 par la fonction f est 2.
Exercices d'application
Notion de fonction – Déterminer l’image et un antécédent par le calcul.pdf
Correction des exercices d’application :
3. Tableau de valeurs
Cours
On considère la fonction f définie à l’aide du tableau :
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| f(x) | -2 | 4 | 0 | 2,7 | -1,6 | 0 | 8 |
L’image de 4 par la fonction f est -1,6.
Les antécédents de 0 par la fonction f sont 2 et 5.
Exercices d'application
Notion de fonction – Déterminer l’image et un antécédent par lecture de tableau.pdf
Correction des exercices d’application :
4. Représentation graphique
Cours
Définition : Soit « x » un nombre et « f(x) » son image par la fonction f.
Dans un repère, la représentation graphique de la fonction f est l’ensemble des points M de coordonnées (x ; f(x) ).
Conséquence :
- Le(s) antécédent(s)d’un nombre se lisent sur l’axe des abscisses.
- L’image d’un nombre se lit sur l’axe des ordonnées.
On considère la fonction f définie par le graphique ci-dessous :
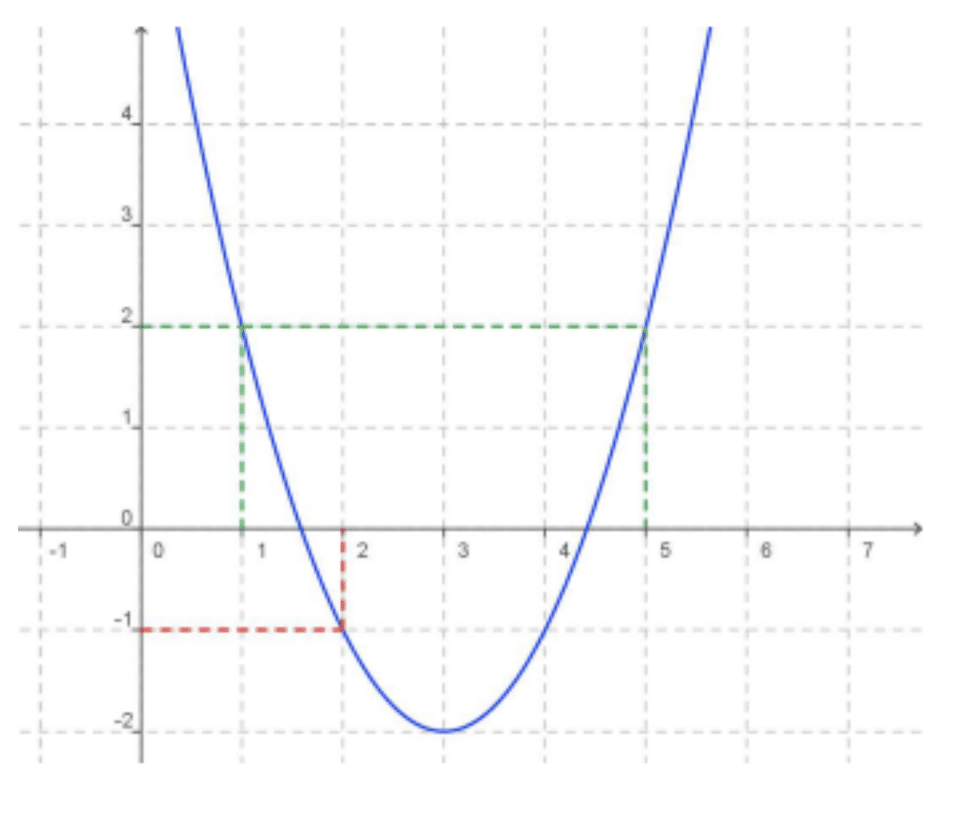
L’image de 2 par la fonction f est -1.
Les antécédents de 2 par la fonction f sont 1 et 5.
Exercices d'application
Notion de fonction – Déterminer l’image et un antécédent par lecture graphique.pdf
Correction des exercices d’application :
Pour plus de vidéos, découvrir la chaine Youtube FormaMaths.
En résumé, ce chapitre vous a permis de comprendre qu’une fonction est comme une « machine » mathématique qui transforme un nombre de départ (l’antécédent) en un nombre d’arrivée (l’image).
Vous avez désormais les clés pour :
Manipuler le vocabulaire : ne plus confondre l’image et l’antécédent.
Utiliser les différentes représentations : passer d’une formule algébrique à un tableau de valeurs ou à une courbe représentative dans un repère.
Calculer et lire graphiquement : savoir trouver un résultat par le calcul ou par la lecture d’un graphique.
La maîtrise des fonctions est essentielle pour le Brevet, mais aussi pour toute votre scolarité au Lycée. C’est un outil puissant pour modéliser le monde réel, que ce soit en physique, en économie ou en informatique.
Prochaines Étapes : De la Théorie à la Pratique
Pour que cette « machine » n’ait plus de secrets pour vous, il n’y a qu’une solution : l’entraînement !
Entraînez-vous avec nos exercices corrigés pour automatiser les calculs d’images et d’antécédents.
Préparez la suite : ce chapitre est la base indispensable avant d’aborder les fonctions linéaires et les fonctions affines et en explorant les autres chapitres de 3ème.
N’hésitez pas à utiliser les ressources complémentaires sur la chaîne Youtube FormaMaths pour des explications visuelles ou bien prendre des cours particuliers. Vous pouvez essayer des maintenant gratuitement et sans condition nos cours particuliers.
