Inégalité triangulaire et construction de triangle 5ème
Le chapitre « inégalité triangulaire et construction de triangle 5ème » est un chapitre important en géométrie.
Un triangle est une figure plane formée par trois segments reliant trois points appelés sommets. Mais toutes les longueurs de segments ne permettent pas de construire un triangle !
Dans ce chapitre, nous allons apprendre :
- La condition pour qu’un triangle existe : l’inégalité triangulaire
- Comment construire un triangle avec des instruments de géométrie
- Différents types de triangles
1. Inégalité triangulaire
Cours
Méthode:
- Repérer le plus grand côté.
- Calculer la somme des longueurs des deux autres côtés.
- Comparer la somme obtenue avec la longueur du plus grand côté
Il y a 3 cas possibles:
1er cas:
2ème cas:
3ème cas:
1er cas:
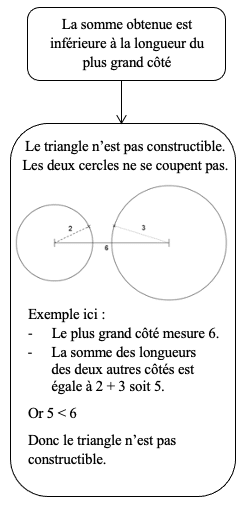
2ème cas:
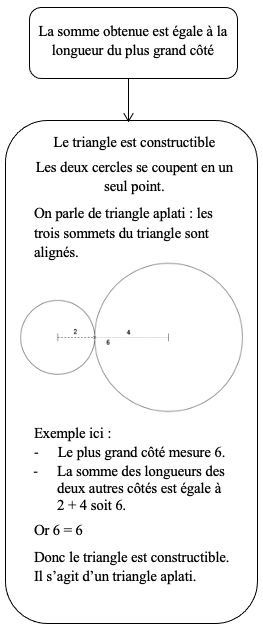
3ème cas:
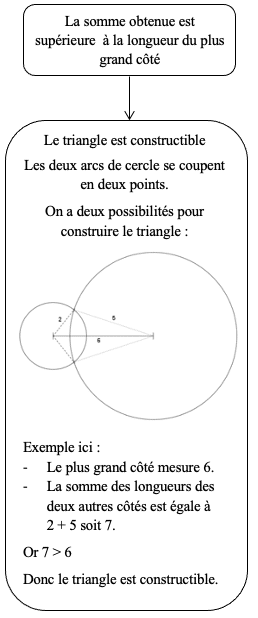
Exercices d'application
Inégalité triangulaire – Dire si un triangle est constructible ou non.pdf
Correction des exercices d’application :
Pour plus de vidéos, découvrir la chaine Youtube FormaMaths.
2. Construction de triangle
Cours
Triangles quelconques
- Connaissant les longueurs des trois cotés
Méthode: Tracer un triangle ABC tel que AB = 6 cm, AC = 4 cm et BC = 5 cm.
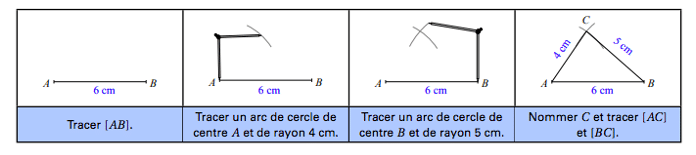
- Connaissant la longueur d’un côté et les deux angles adjacents à ce côté
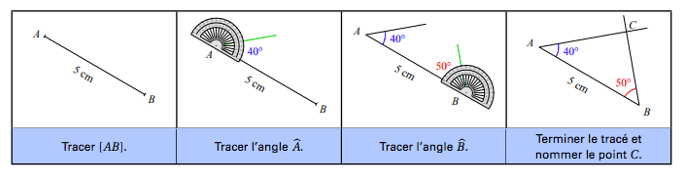
Méthode: Tracer un triangle ABC tel que AB = 5 cm, BÂC = 40° et ABC = 50°.
- Connaissant un angle et les longueurs des deux côtés qui lui sont adjacents
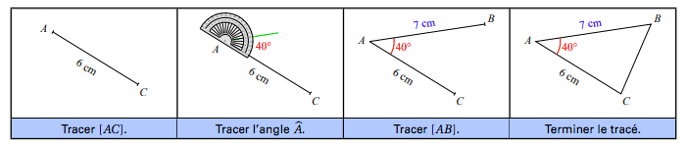
Méthode: Tracer un triangle ABC tel que BÂC = 40° , AC = 6 cm et AB = 7 cm.
- Connaissant un angle et deux côtés qui ne lui sont pas adjacents
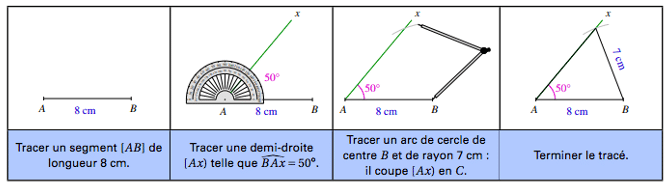
Méthode: Tracer un triangle ABC tel que AB = 8 cm, BC = 7 cm et BÂC = 50°.
Triangles isocèles
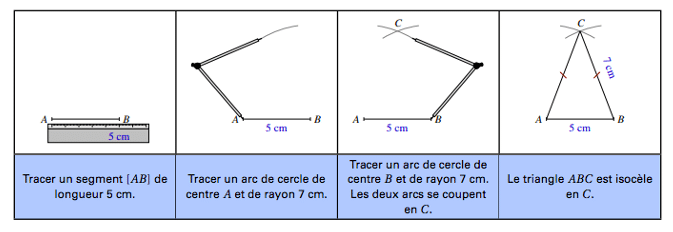
Méthode: Tracer un triangle ABC isocèle en C tel que AB = 5 cm et AC = 7 cm.
Triangles rectangles
- Connaissant les deux côtés de l’angle droit.
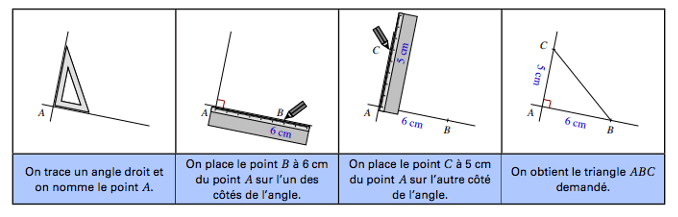
Méthode: Tracer un triangle ABC rectangle en A tel que AB = 6 cm et AC = 5 cm.
- Connaissant un côté de l’angle droit et l’hypoténuse.
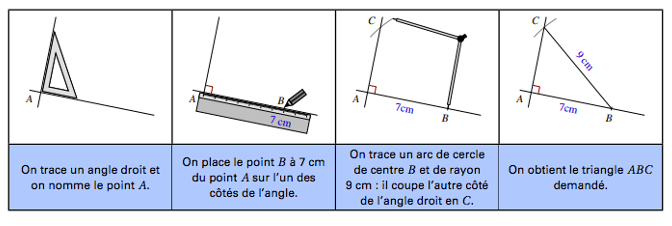
Méthode: Tracer un triangle ABC rectangle en A tel que AB = 7 cm et BC = 9 cm.
En résumé, ce chapitre « inégalité triangulaire et construction de triangle 5ème » vous a enseigné que :
L’Inégalité Triangulaire est la condition d’existence d’un triangle : la somme des longueurs des deux plus petits côtés doit toujours être supérieure (ou égale, dans le cas d’un triangle aplati) à la longueur du plus grand côté. C’est l’étape incontournable pour savoir si une construction est possible.
La Construction de triangle dépend des informations fournies (trois côtés, un côté et deux angles, un angle et deux côtés adjacents, etc.). Vous savez maintenant utiliser vos outils de géométrie (règle et compas) pour tracer avec précision un triangle quelconque, isocèle ou rectangle.
Ces notions sont les fondations de toute la géométrie future. Savoir si un triangle est constructible et comment le tracer est la première étape vers la résolution de problèmes plus complexes.
Prochaines Étapes
La géométrie est une question de méthode et de précision. Pour exceller :
Révisez l’Inégalité triangulaire pour qu’elle devienne un réflexe avant toute construction.
Entraînez-vous à construire différents types de triangles en vous concentrant sur la justesse des mesures et des angles.
Poursuivez votre exploration des autres chapitres de 5ème, notamment les notions d’angles et de parallélisme.
Continuez à vous entraîner en visitant la chaîne Youtube FormaMaths pour des supports visuels supplémentaires ou bien prendre des cours particuliers. Vous pouvez essayer des maintenant gratuitement et sans condition nos cours particuliers.
