Solides 3ème
Le chapitre « Solides 3ème » est un chapitre de géométrie qui tombe très souvent lors de l’épreuve de mathématiques du Diplôme du Brevet du Collège.
Un solide est une figure en trois dimensions qui occupe un espace. Contrairement aux figures planes comme le carré ou le cercle, les solides ont une longueur, une largeur et une hauteur.
Dans ce chapitre, nous allons découvrir les différents types de solides, leurs caractéristiques principales, ainsi que les formules pour calculer leur volume et leur surface.
1. Définition de solides
Cours
Pavé droit ou Parallélépipède rectangle
Définition: Un pavé droit ou parallélépipède rectangle est un solide qui possède 6 faces et 12 arrêtes.
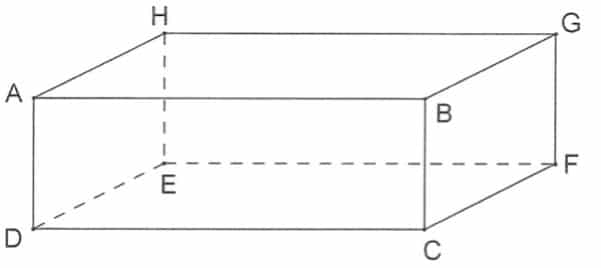
Nom : ABCDHGFE
Nom de ses faces : ABCD ; HGFE ; AHED ; BGFC ; AHGB ; DEFC
Nom de ses arêtes : [AD] ;[BC] ; [GF] ; [HE] ; [AH] ; [BG] ; [DE] ; [CF] ; [AB] ; [HG] ;[DC] ;[EF]
Cube
Définition: Un cube est un parallélépipède rectangle dont toutes les faces sont des carrés
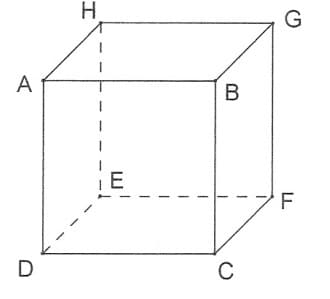
Remarque : Tous les côtés sont égaux.
Prisme droit
Définition: Un prisme droit est un solide dont :
- deux faces sont des polygones (triangle, quadrilatère…etc) identiques et parallèles on les appelle les bases
- les autres faces sont des rectangles ; on les appelle les faces latérales

Nom : ABCFED
Nom de ses bases : ABC ; FED
Nom de ses faces latérales : ABEF ; ACDF ; BCDE
Nom de ses arêtes latérales : [AF] ; [CD] ; [BE]
Nom : ABCDHGFE
Nom de ses bases : ABCD ; HGFE
Nom de ses faces latérales : ABGH ; BCFG ; CDEF ; ADEH
Nom de ses arêtes latérales : [AH] ; [BG] ; [CF] ; [DE]
Remarques :
- Les arêtes latérales d’un prisme droit sont des segments parallèles et de même longueur.
- La hauteur d’un prisme droit est la longueur de ses arêtes latérales.
Cylindre
Définition: Un cylindre de révolution est un solide qui possède :
- Deux faces identiques et parallèles qui sont des disques. On les appelle les bases
- Une face latérale dont le patron est un rectangle.
Remarque : Un cylindre de révolution est un solide décrit par un axe qui tourne autour de l’un de ses côtés.
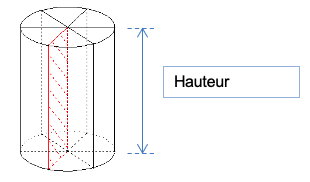
La hauteur d’un cylindre est la longueur du segment reliant les centres de ses deux bases.
Pyramide
Définition: Une pyramide est un solide constitué :
- D’une face rectangulaire appelée base de la pyramide
- De faces triangulaires qui ont un sommet commun, appelé sommet de la pyramide. Ces faces sont appelées faces latérales.
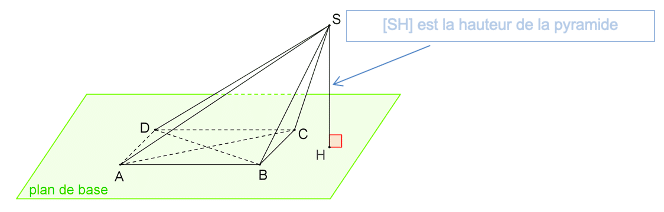
Nom : SABCD
Nom de son sommet : S
Nom de sa base : ABCD
Nom de ses faces latérales : SAD ; SAB ; SBC ; SCD
Nom de ses arêtes latérales : [SA] ; [SB] ; [SC] ; [SD]
Remarque : Une pyramide dont la base est un triangle est un tétraèdre.
- Cas particulier : La pyramide régulière
Définition: Une pyramide régulière est une pyramide telle que :
- Sa base soit un polygone. (Triangle équilatéral, carré, pentagone, hexagone … etc)
- Son sommet se trouve sur la droite perpendiculaire au plan de base passant par le centre de la base.
Remarque :
- Le centre d’un triangle équilatéral est le centre de gravité de ce triangle.
- Le centre d’un carré est le point d’intersection de ses diagonales.
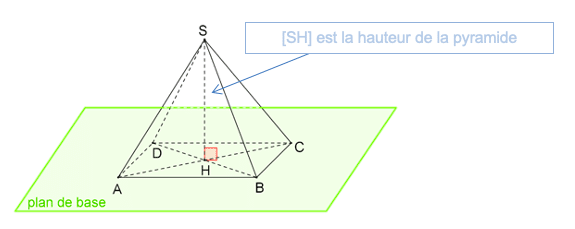
Remarque : Pour une pyramide régulière:
- Les arêtes latérales ont la même longueur
- Les faces latérales sont des triangles isocèles et superposables
Cône
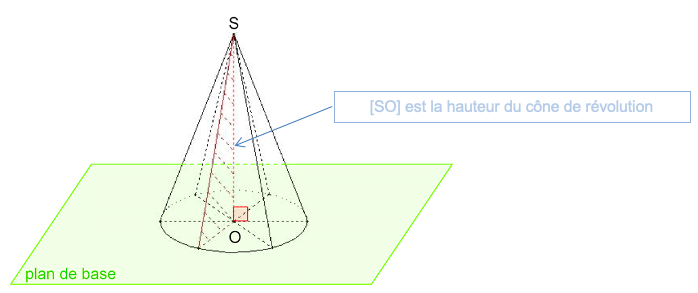
Définition: Un cône est un solide constitué :
- D’un cercle qui constitue sa base.
- D’une seule face latérale.
Un cône est dit de « révolution » lorsque son sommet se trouve sur la droite perpendiculaire au plan de base passant par le centre du disque de base.
Sphère
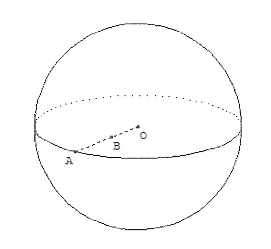
Définition: Une sphère de centre O et de rayon est l’ensemble des points M de l’espace tel que OM = r.
Exemple : La balle de tennis de table
Soit « S », la sphère ci-contre de centre O et de rayon 2 cm.
Le point A appartient à « S » car OA = 2.
Le point B n’appartient pas à « S » car OB < 2.
Définitions :
Un diamètre d’une sphère est un segment reliant deux points de cette sphère et passant par son centre.
Un grand cercle d’une sphère est un cercle de même centre et de même rayon que cette sphère.
Boule
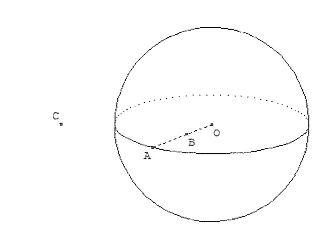
Définition: Une boule de centre O et de rayon est l’ensemble des points M de l’espace tel que OM ≤ r.
Exemple : La boule de billard
Soit « B1 », la boule ci-contre de centre O et de rayon 2 cm.
Le point A appartient à « B1 » car OA = 2.
Le point B appartient à « B1 » car OB < 2.
Le point C n’appartient pas à « B1 » car OC > 2.
2. Aire - Formules
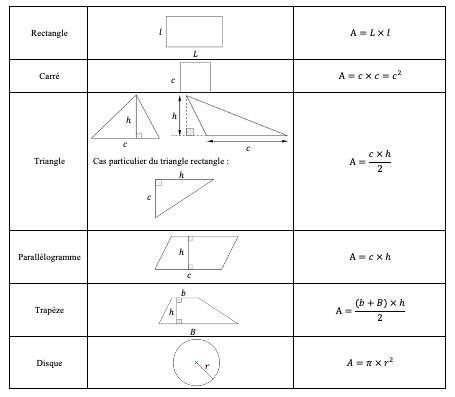
3. Volume - Formules
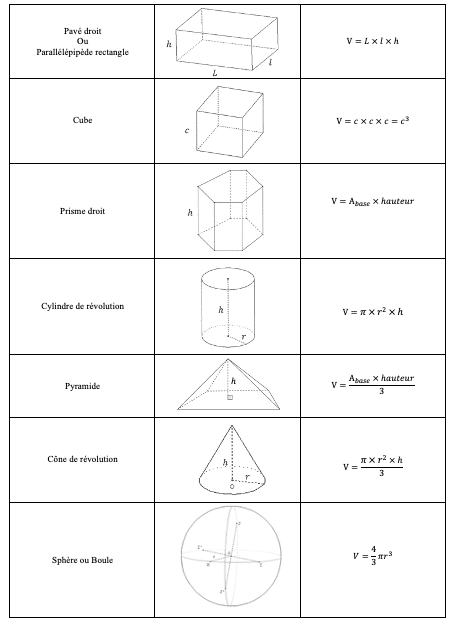
Exercices d'application
Solides – Calcul de volumes.pdf
Correction de l’exercice 1 d’application :
Correction de l’exercice 2 d’application :
Correction de l’exercice 3 d’application :
Pour plus de vidéos, découvrir la chaine Youtube FormaMaths.
Grâce à ce chapitre « solides 3ème » , nous avons appris à reconnaître et classer les solides, ainsi qu’à calculer leur volume et leur aire.
La géométrie des solides est essentielle dans de nombreux domaines comme l’architecture, la physique et l’ingénierie !
Prochaines Étapes
La pratique régulière est essentielle pour se familiariser avec les solides. Pour exceller :
Révisez attentivement les exercices corrigés pour vous familiariser.
Poursuivez votre progression en explorant les autres chapitres de 3ème.
N’hésitez pas à utiliser les ressources complémentaires sur la chaîne Youtube FormaMaths pour des explications visuelles ou bien prendre des cours particuliers. Vous pouvez essayer des maintenant gratuitement et sans condition nos cours particuliers.
