Théorème de Thalès 3ème
Le théorème de Thalès en 3ème est un des théorèmes fondamentaux de la géométrie. Il permet de calculer des longueurs dans des figures contenant des droites parallèles et des triangles. Ce théorème est particulièrement utile en cartographie, en architecture et en astronomie.
Dans ce chapitre, nous allons découvrir :
- Les conditions d’application du théorème de Thalès
- La relation de proportionnalité entre les longueurs
- Des exemples et exercices pour bien comprendre
1. Calculer une longueur
Cours
Énoncé du théorème de Thalès
Théorème :
Soient (BN) et (CM) deux droites sécantes en A. Si les droites (MN) et (BC) sont parallèles, alors :
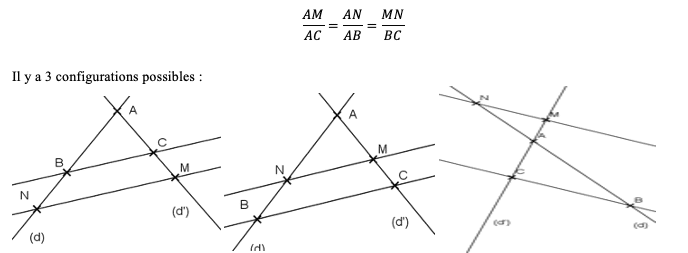
Remarque: Le théorème de Thalès permet de calculer des longueurs.
Application
Dans la figure ci-dessous les droites (FE) et (ST) sont parallèles.
On a : FK = 6cm, SK = 3 cm, KT = 2 cm et FE = 9,3 cm.
Calculer KE et ST.
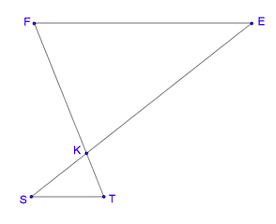
Correction :
On sait que :
- Les droites (FT) et (SE) sont sécantes en K
- Les droites (FE) et (ST) sont parallèles
Donc d’après le théorème de Thalès :

Exercices d'application
Théorème de Thalès – Calculer une longueur.pdf
Correction des exercices d’application :
2. Démontrer que des droites sont parallèles ou non
Cours
Énoncé
Réciproque du théorème de Thalès:
Si AM/AB = AN/AC et si les points A, M et B sont alignés dans le même ordre que les points A, N et C, alors les droites (MN) et (BC) sont parallèles.
Application
Sur la figure ci-dessous, les droites (VG) et (HJ) sont-elles parallèles ?
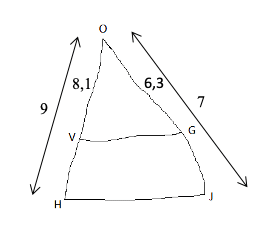
Correction :
- Les points O, V et H sont alignés dans le même ordre que les points O, G et J.
- On a : OV/OH = 8,1/9 = 0,9 et OG/OJ = 6,3/7 = 0,9
Donc : OV/OH = OG/OJ
Donc d’après la réciproque du théorème de Thalès, les droites (VG) et (HJ) sont parallèles.
Exercices d'application
Théorème de Thalès – Démontrer que des droites sont parallèles ou non.pdf
Correction des exercices d’application :
Pour plus de vidéos, découvrir la chaine Youtube FormaMaths.
Le chapitre du théorème de Thalès en 3ème vous a donné les clés pour :
Calculer des longueurs (Théorème direct) : En présence de deux droites sécantes coupées par deux droites parallèles, vous pouvez utiliser la relation de proportionnalité pour déterminer des mesures inconnues.
Démontrer le parallélisme (Réciproque) : En vérifiant que les rapports de longueurs sont égaux et que les points sont alignés dans le même ordre, vous pouvez prouver que deux droites sont parallèles.
Le Théorème de Thalès est un outil puissant qui permet de résoudre de nombreux problèmes pratiques en mesurant indirectement des distances (hauteurs d’objets, largeur de rivières, etc.).
Prochaines Étapes
La pratique régulière est essentielle pour intégrer la logique de Thalès et de sa réciproque. Pour exceller :
Révisez attentivement les exercices corrigés pour vous familiariser avec les différentes configurations (triangle emboîté et papillon).
Poursuivez votre progression en explorant les autres chapitres de 3ème, notamment ceux qui traitent de la trigonométrie et des notions de volumes, où la géométrie est omniprésente.
N’hésitez pas à utiliser les ressources complémentaires sur la chaîne Youtube FormaMaths pour des explications visuelles ou bien prendre des cours particuliers. Vous pouvez essayer des maintenant gratuitement et sans condition nos cours particuliers.
