Fractions 5ème
Le chapitre « Fractions 5ème » permet d’apprendre à additionner, soustraire, multiplier, simplifier et comparer les fractions avec aisance et comprendre leur utilité dans la vie de tous les jours.
Une fraction est une manière d’écrire une division entre deux nombres. Elle permet d’exprimer une partie d’un tout. Par exemple, si on partage une pizza en 4 parts égales, alors 1 part représente la fraction : 1/4
Les fractions sont utilisées en cuisine, en mathématiques, en physique et dans de nombreux domaines du quotidien.
Dans ce chapitre, nous allons apprendre :
- Ce qu’est une fraction et comment la lire
- Les types de fractions
- Comment additionner, soustraire, multiplier et diviser des fractions
1. Définitions
Cours
Un nombre rationnel est un nombre qui peut s’écrire sous la forme d’une fraction.
Une fraction est un quotient de deux nombres entiers.
Exemple : 2 = 2/1 ; 0,5 = 1/2 et 10/3 sont des nombres rationnels.
Une fraction peut être utilisée pour représenter un partage à parts égales.
Exemple :

Le rectangle est partagé en 5 parts égales. Il y a 2 parts coloriées. La fraction qui représente ce partage est donc de 2/5.
2. Deux fractions égales
Propriété : Deux fractions sont égales quand leurs numérateurs et dénominateurs sont proportionnels.
Pour tout nombre a, b et k où b et k sont non nuls :
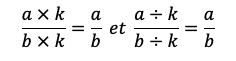
Exemple : Déterminer le nombre manquant.
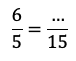
Afin de trouver le nombre manquant, il faut commencer par trouver la table de multiplication qui permet de passer d’une fraction à l’autre. Ici, c’est la table de 3 car 5 x 3 = 15.
Ensuite, il faut multiplier le numérateur par 3 également afin d’obtenir le nombre manquant et avoir les fractions égales. Le nombre manquant est donc18 car 6 x 3 =18.
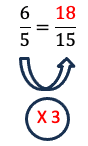
3. Simplifier une fraction
Méthode : Il s’agit de trouver une fraction égale ayant un dénominateur (entier) plus petit.
Exemple : Simplifier les fractions suivantes : 15/21 et 72/48.
- Pour simplifier la fraction 15/21, il faut trouver une table de multiplication qui a pour résultat 15 et 21. Ici, c’est la table de 3. Il suffit de simplifier par 3 comme ceci.
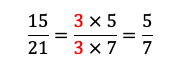
Pour simplifier la fraction 72/48, il faut trouver une table de multiplication qui a pour résultat 72 et 48. Ici, c’est la table de 24. Il suffit de simplifier par 24 comme ceci.
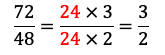
Si on ne trouve pas la table de 24 directement, on peut aussi effectuer la simplification en 2 étapes. On peut voir que la table de 8 a pour résultat 72 et 48. On commence donc par simplifier par 8 puis voir que 9 et 6 sont des résultats de la table de 3 et donc simplifier par 3 comme ceci.
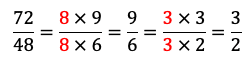
Exercices d'application
Fractions – Simplifier une fraction.pdf
Correction des exercices d’application :
4. Comparer des fractions
Une fraction est supérieure à 1 lorsque le numérateur est plus grand que le dénominateur (Exemple : 5/4 >1).
Une fraction est inférieure à 1 lorsque le numérateur est plus petit que le dénominateur (Exemple : 4/5 <1).
Elle est égale à 1 lorsque le numérateur est égal au dénominateur (Exemple : 5/5 =1).
Méthode : Pour comparer des fractions, on peut les comparer par rapport à 1 ou bien, on peut les écrire avec le même dénominateur pour ensuite pouvoir comparer les numérateurs.
Exemple 1: Comparer les fractions suivantes : 15/21 et 72/48.
15/21 est une fraction inférieure à 1 car le numérateur est plus petit que le dénominateur.
72/48 est une fraction supérieure à 1 car le numérateur est plus grand que le dénominateur.
Donc 15/21 < 72/48.
Exemple 2: Comparer les fractions suivantes : 3/7 et 8/21.
Pour comparer les fractions ci-dessus, il faut tout d’abord mettre les fractions au même dénominateur puis comparer les numérateurs.
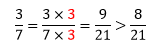
Donc 3/7 > 8/21.
Exemple 3: Ranger les fractions suivantes dans l’ordre croissant : 3/20 ; 4/4 ; 12/40 ; 7/40 ; 5/10.
Pour pouvoir classer les fractions, il faut tout d’abord mettre toutes les fractions au même dénominateur. (Ici sur 40)
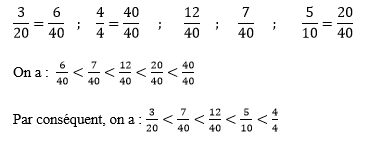
Exercices d'application
Fractions – Comparer des fractions.pdf
Correction des exercices d’application :
Pour plus de vidéos, découvrir la chaine Youtube FormaMaths.
Ce chapitre « Fractions 5ème » vous a permis de comprendre :
La définition d’une fraction et sa représentation comme un partage ou un nombre rationnel.
La propriété d’égalité qui permet de trouver des fractions équivalentes.
La méthode pour simplifier une fraction et la rendre irréductible.
Les techniques pour comparer et ranger différentes fractions.
La maîtrise des fractions est cruciale car elle sert de base à de nombreux concepts mathématiques futurs.
Prochaines Étapes
Pour transformer cette compréhension théorique en un véritable savoir-faire, il est indispensable de pratiquer régulièrement. Nous vous recommandons de :
Refaire les exercices corrigés pour automatiser les méthodes de simplification et de comparaison.
Continuer d’explorer les autres chapitres de 5ème pour lier les fractions aux nombres décimaux, aux pourcentages et à la proportionnalité.
N’hésitez pas à consulter la chaîne Youtube FormaMaths pour des supports vidéo supplémentaires ou bien prendre des cours particuliers. Vous pouvez essayer des maintenant gratuitement et sans condition nos cours particuliers.
