Trigonométrie 3ème
La trigonométrie 3ème permet de calculer des longueurs et des angles dans un triangle rectangle en utilisant les rapports trigonométriques (sinus, cosinus, tangente).
Rappel : Le Triangle Rectangle
Un triangle rectangle est un triangle qui possède un angle droit (90°). Les côtés de ce triangle portent des noms spécifiques :
- L’hypoténuse : c’est le côté le plus long, situé en face de l’angle droit.
- Le côté opposé : c’est le côté situé en face de l’angle étudié.
- Le côté adjacent : c’est le côté qui est à la fois collé à l’angle étudié et qui n’est pas l’hypoténuse.
1. Cosinus, sinus et tangente d'un angle aigu dans un triangle rectangle
Cours
Définition : Le triangle ABC rectangle en B ci-dessous possède deux angles aigus et
Pour chacun de ces angles, on définit un côté adjacent et un côté opposé :
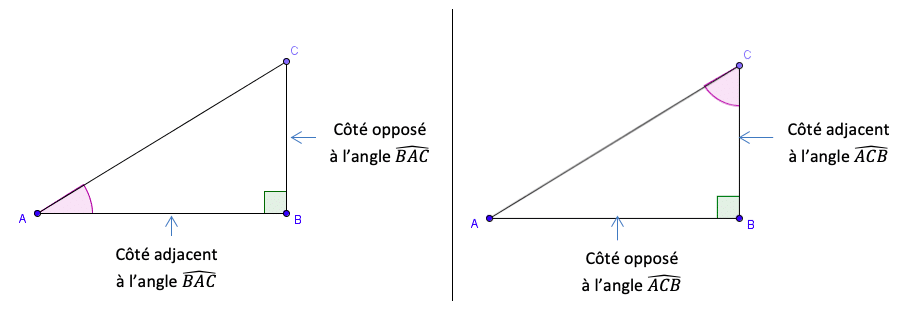
À chacun de ces angles aigus, on fait correspondre trois nombres appelés cosinus, sinus et tangente de l’angle.
Formules de trigonométrie :
Dans un triangle rectangle, on a :
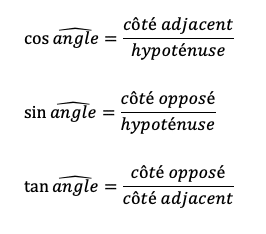
Remarque: Afin de retrouver facilement ces formules, on utilise l’expression :

Le cosinus, le sinus et la tangente sont trois rapports de longueurs, ils sont donc sans unités.
De plus, l’hypoténuse étant le plus long côté, le cosinus et le sinus sont donc inférieurs à 1.
2. Applications de la trigonométrie
Cours
Calcul de longueurs
Méthode : Calculer la longueur IE. Vous donnerez un arrondi au millimètre.
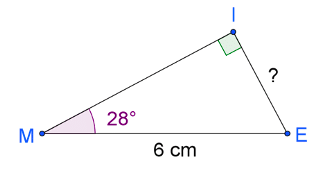
Réponse :
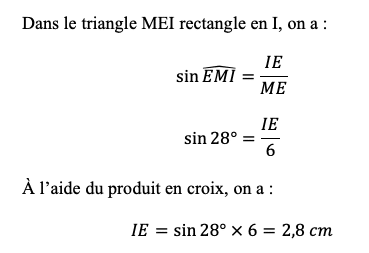
Exercices d'application
Trigonométrie – Calcul de longueurs.pdf
Correction des exercices d’application :
Pour plus de vidéos, découvrir la chaine Youtube FormaMaths.
Cours
Calcul d'angles
Méthode : Calculer la mesure de l’angle aigu (rose). Donner un arrondi au degré près.
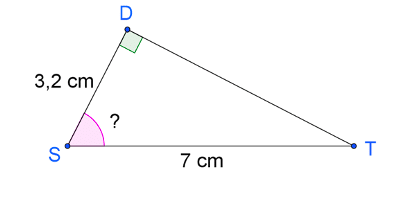
Réponse :

Exercices d'application
Trigonométrie – Calcul d’angles.pdf
Correction des exercices d’application :
Pour plus de vidéos, découvrir la chaine Youtube FormaMaths.
En résumé, nous venons de voir que grâce aux fonctions trigonométriques, on peut :
- Calculer une longueur inconnue dans un triangle rectangle.
- Déterminer un angle inconnu à l’aide des fonctions trigonométriques inverses (arcsin, arccos, arctan).
- Appliquer la trigonométrie en physique pour calculer des hauteurs, des distances, ou analyser des mouvements.
En maîtrisant ces notions, on pourra ensuite les appliquer, à partir du lycée, à des notions plus avancées comme les angles dans un cercle, la trigonométrie dans l’espace et même les ondes en physique.
Prochaines Étapes
La pratique régulière est essentielle pour se familiariser avec la trigonométrie. Pour exceller :
Révisez attentivement les exercices corrigés pour vous familiariser.
Poursuivez votre progression en explorant les autres chapitres de 3ème.
N’hésitez pas à utiliser les ressources complémentaires sur la chaîne Youtube FormaMaths pour des explications visuelles ou bien prendre des cours particuliers. Vous pouvez essayer des maintenant gratuitement et sans condition nos cours particuliers.
