Théorème de Pythagore 4ème
Le théorème de Pythagore en 4ème est l’un des théorèmes les plus importants en géométrie. Il permet de calculer des longueurs dans un triangle rectangle, c’est-à-dire un triangle qui possède un angle droit (90°).
Ce théorème est très utile en mathématiques, en physique, en architecture et dans de nombreux domaines scientifiques.
Dans ce chapitre, nous allons apprendre :
- L’énoncé du théorème de Pythagore
- Comment l’utiliser pour calculer une longueur inconnue
- Sa réciproque pour vérifier si un triangle est rectangle
1. Calculer une longueur
Cours
Énoncé du théorème de Pythagore
Ce théorème permet de calculer une longueur dans un triangle rectangle quand on connait les deux autres.
Théorème : Si un triangle est rectangle alors la longueur au carré de l’hypoténuse est égale à la somme des longueurs au carré des deux autres côtés.
Définition : Un triangle rectangle est un triangle qui a un angle droit. L’hypoténuse est le plus grand côté dans un triangle rectangle (C’est le côté opposé à l’angle droit).
Applications
- On considère un triangle ABC rectangle en A tel que AB=4cm et AC=3cm.

Quelle est la longueur du segment [BC] ?
1er cas : On cherche la longueur de l’hypoténuse.
On sait que le triangle ABC est rectangle en A.
Or d’après le théorème de Pythagore on a :
BC² = AB² + AC²
BC² = 4² + 3²
BC² = 16 + 9
BC² = 25
BC = √25 = 5
Donc la longueur du segment [BC] est de 5cm.
2. On considère le triangle EFH rectangle en E, tel que EF=8cm et FH=20cm.
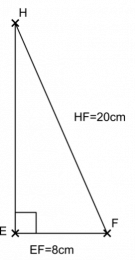
Quelle est la longueur du segment [EH] ?
2ème cas : On cherche la longueur d’un des côtés de l’angle droit.
On sait que le triangle EFH est rectangle en E.
Or d’après le théorème de Pythagore on a :
HF² = EF² + EH²
20² = 8² + EH²
400 = 64 + EH²
EH² = 400 – 64 = 336
EH² = 336
EH = √336 ≈18,3cm
Donc la longueur du segment [EH] est d’environ 18,3cm.
Exercices d'application
Théorème de Pythagore – Calculer une longueur.pdf
Correction des exercices d’application :
2. Démontrer qu'un triangle est rectangle ou non
Cours
Énoncé
Propriété : Soit ABC un triangle dont [BC] est le plus grand côté.
Si on a BC² = AB² + AC², alors le triangle ABC est rectangle en A.
Cette propriété correspond à la réciproque du théorème de Pythagore.
Applications
1. Le triangle SET tel que ET = 13 cm, SE = 5 cm et ST = 12 cm est-il rectangle ?
On sait que : [ET] est le plus grand côté.
D’une part : D’autre part :
ET² = 13² SE² + ST² = 5² + 12²
ET² = 169 SE² + ST² = 25 + 144 = 169
On remarque que : ET² = SE² + ST²
L’égalité de Pythagore est vérifiée.
Donc le triangle SET est rectangle en S.
2. Le triangle IJK tel que IK = 28 cm, IJ = 20 cm et JK = 21 cm est-il rectangle ?
On sait que : [IK] est le plus grand côté.
D’une part : D’autre part :
IK² = 28² IJ² + JK² = 20² + 21²
IK² = 784 IJ² + JK² = 400 + 441 = 841
On remarque que : IK² ≠ IJ² + JK²
L’égalité de Pythagore n’est pas vérifiée.
Donc le triangle IJK n’est pas rectangle.
1. Le triangle SET tel que ET = 13 cm, SE = 5 cm et ST = 12 cm est-il rectangle ?
On sait que : [ET] est le plus grand côté.
D’une part :
ET² = 13²
ET² = 169
D’autre part :
SE² + ST² = 5² + 12²
SE² + ST² = 25 + 144 = 169
On remarque que : ET² = SE² + ST²
L’égalité de Pythagore est vérifiée.
Donc le triangle SET est rectangle en S.
2. Le triangle IJK tel que IK = 28 cm, IJ = 20 cm et JK = 21 cm est-il rectangle ?
On sait que : [IK] est le plus grand côté.
D’une part :
IK² = 28²
IK² = 784
D’autre part :
IJ² + JK² = 20² + 21²
IJ² + JK² = 400 + 441 = 841
On remarque que : IK² ≠ IJ² + JK²
L’égalité de Pythagore n’est pas vérifiée.
Donc le triangle IJK n’est pas rectangle.
Exercices d'application
Théorème de Pythagore – Démontrer qu’un triangle est rectangle ou non.pdf
Correction de l’exercice d’application :
Pour plus de vidéos, découvrir la chaine Youtube FormaMaths.
En résumé, vous avez appris deux applications fondamentales :
Calculer une longueur : Le théorème direct vous permet de déterminer la longueur de l’hypoténuse ou d’un côté de l’angle droit dans un triangle rectangle dès que vous connaissez les longueurs des deux autres côtés.
Prouver un angle droit : La réciproque du théorème de Pythagore est l’outil indispensable pour démontrer qu’un triangle est, ou n’est pas, un triangle rectangle.
L’élément essentiel à retenir est d’identifier correctement l’hypoténuse (le plus grand côté, toujours opposé à l’angle droit) pour bien appliquer la formule.
Prochaines Étapes
Pour maîtriser ce théorème, la pratique est la clé.
Révisez les exercices corrigés pour vous assurer que l’application de la formule et de la réciproque est un réflexe.
Poursuivez votre exploration avec les autres chapitres de 4ème notamment ceux qui préparent à la trigonométrie et au Théorème de Thalès.
Continuez à vous entraîner en visitant la chaîne Youtube FormaMaths pour des explications complémentaires et des supports visuels ou bien prendre des cours particuliers. Vous pouvez essayer des maintenant gratuitement et sans condition nos cours particuliers.
